역전파에 대한 강의나 수식이 비전공자인 나에게 잘 와닿지 않아 내가 이해한 가장 간단하고 쉬운 방법으로 역전파의 미분을 정리해보았다.
역전파는 신경망의 각 노드가 가지고 있는 가중치(Weight)와 편향(Bias)을 학습시키기 위한 알고리즘 목표(Target)와 모델의 예측 결과(Output)가 얼마나 차이가 나는지 확인하고 그 오차를 바탕으로 가중치와 편향을 뒤에서부터 앞으로 갱신해가는 것을 의미한다. 역전파란 명칭도 바로 이처럼 뒤에서부터 다시 앞으로 거슬러 올라간다는 것에서 나온 것이다.
위 과정을 이해하려면 미분에 대해 알아야 한다.
미분
미분은 함수 ff의 주어진 점 (x,f(x))(x,f(x))에서의 접선의 기울기를 구하는 과정이다.
y증가량/ x증가량
좀 더 간단히, 위 그림을 두고 말하자면 f에 대한 X의 미분을 구한다는건 X가 h만큼 변했을때 f는 얼만큼의 변화량을 갖는가를 의미한다. (f를 최종 출력 값으로 간주)
- 덧셈 노드의 미분은 1이다.
- y * z = f 일 때 곱셈 노드의 y미분은 z이다. (반대도 마찬가지 z 미분은 y)
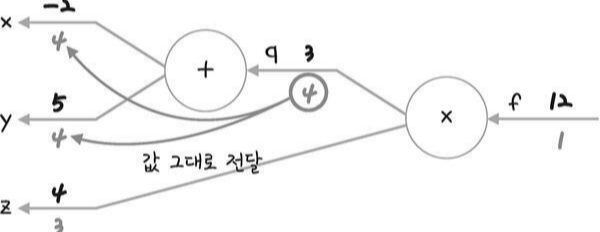
그림과 같이 (x+y) * z = f -> ( -2 + 5 ) * 4 = 12 에서 f에 대한 x의 미분값을 구한다는 의미는 x 변화량에 따른 y 변화량을 구하겠다는 의미이다. $$\frac{af}{ax}$$
X 를 -1 이라고 가정했을 때 X의 변화량은 -2 에서 -1 로 1이 된다. 식에 대입해보면 ( -1 + 5 ) * 4 = 16 , X가 1 변했을 때 f 는 12에서 16으로 4 변화량이 생겼다. (X를 -2에서 -3으로 바꿔 계산해도 f의 변화량은 4이다.)
즉 f에 대한 X의 미분값은 4가 된다.
좀 더 자세히, 역전파는 순전파의 반대의 과정으로 맨끝 부터 처음까지 거슬러 올라가는 (upstream) 방식으로 진행된다.
즉 x미분을 구하고자 한다면 q미분 -> x미분을 구하는 것이 순서이다.q의 미분은 af/aq 가 된다. 곱셈 노드의 특성상 q의 미분값은 z값이 된다.$$\frac{af}{aq} = z $$
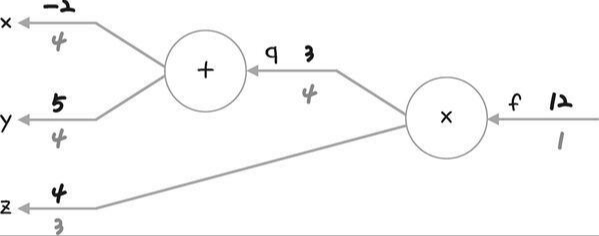
다시 정리하면 X에 대한 미분을 구하는 공식은 아래와 같다.
$$\frac{aq}{ax} * \frac{af}{aq}= 1 * 4$$
덧셈 노드의 미분 =1, af/aq = z = 4

'딥러닝(DL)' 카테고리의 다른 글
| Word-Embedding - Embedding Layer (0) | 2022.07.24 |
|---|---|
| Word-Embedding (0) | 2022.07.24 |
| 성능 개선을 위한 regularization 기법들 (0) | 2022.07.10 |
| Loss Function, Cost Function, Objective Function의 차이 (0) | 2022.06.26 |


댓글